1087. Скобочная последовательность

Определим правильное скобочное выражение следующим образом:

1. Пустое выражение – правильное.

2. Если выражение S правильное, то (S) и [S] также правильные.

3. Если выражения A и B правильные, то и выражение AB правильное.

Дана последовательность скобок (, ), [, и ]. Требуется найти самое короткое правильное выражение, в котором данная последовательность является подпоследовательностью, то есть такое, из которого можно вычеркнуть некоторые символы (возможно, ноль) и получить исходную последовательность, не меняя порядок оставшихся.

Вход. В первой строке находятся символы (, ), [, и ] без пробелов. Исходная последовательность содержит не более 100 скобок.

Выход. Вывести искомую последовательность скобок без пробелов.

Пример входа	Пример выхода
([(]	()[()]

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть S = s₀s₁…s_n-1 – входная строка. Пусть dp[i][j] равно наименьшему количеству символов, которое следует вставить в подстроку s_i…s_j так чтобы она стала правильной. Очевидно, что dp[i][i] = 1 независимо от типа скобки s_i. При i > j положим dp[i][j] = 0. Далее будем писать s_i ≈ s_j, если s_i – открывающаяся, а s_j – соответствующая закрывающаяся скобка.

· Если s_i ≈ s_j, то dp[i][j] = min(dp[i][j], dp[i + 1][j – 1]);

· Если s_i ≠ s_j, то dp[i][j] = (dp[i][j], dp[i][k] + dp[k + 1][j]);

В массиве p будем хранить информацию для восстановления результирующей строки. Положим

· p[i][j] = -1, если s_i ≈ s_j и минимум dp[i][j] достигается на dp[i + 1][j – 1];

· p[i][j] = k, если минимум dp[i][j] достигается на слагаемом dp[i][k] + dp[k + 1][j];

Пример

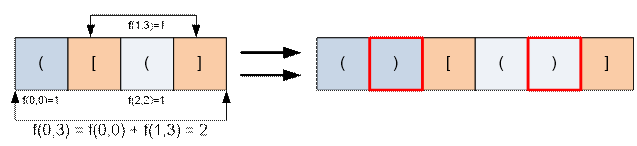
Реализация алгоритма

Определим константы и рабочие массивы.

#define MAX 110

#define INF 0x3F3F3F3F

char s[MAX];

int dp[MAX][MAX], p[MAX][MAX];

Вывод результирующей строки с i-ой позиции до j-ой.

void Print(int i, int j)

{

if (i > j) return;

if (i == j)

{

if (s[i] == '(' || s[i] == ')')

printf("()");

else

printf("[]");

} else if (p[i][j] == -1)

{

printf("%c", s[i]);

Print(i + 1, j - 1);

printf("%c", s[j]);

} else

{

Print(i, p[i][j]);

Print(p[i][j] + 1, j);

}

}

При помощи функции Solve(i, j) вычисляем в dp[i][j] наименьшее количество символов, которое следует вставить в подстроку s_i…s_j так чтобы она стала правильной. Одновременно заполняем ячейки массива p для восстановления результирующей строки.

int Solve(int i, int j)

{

if (i == j) return 1;

if (i > j) return 0;

if (dp[i][j] != INF) return dp[i][j];

if ((s[i] == '(' && s[j] == ')') || (s[i] == '[' && s[j] == ']'))

dp[i][j] = min(dp[i][j], Solve(i+1,j-1));

for (int k = i; k < j; k++)

{

int temp = Solve(i,k) + Solve(k+1,j);

if (temp < dp[i][j])

{

p[i][j] = k;

dp[i][j] = temp;

}

}

return dp[i][j];

}

Основная часть программы. Читаем строку s.

gets(s); len = strlen(s);

memset(dp,0x3F,sizeof(dp));

memset(p,-1,sizeof(p));

Вычисляем и выводим ответ.

Solve(0, len - 1);

print(0, len - 1);

printf("\n");